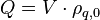Homogeneous charge density
For the special case of a homogeneous charge density, that is one that is independent of position, equal to ρq,0 the equation simplifies to:
The proof of this is simple. Start with the definition of the charge of any volume:
Then, by definition of homogeneity,  is a constant that we will denote ρq,0 to differentiate between the constant and non-constant forms, and thus by the properties of an integral can be pulled outside of the integral resulting in:
is a constant that we will denote ρq,0 to differentiate between the constant and non-constant forms, and thus by the properties of an integral can be pulled outside of the integral resulting in:
so,
The equivalent proofs for linear charge density and surface charge density follow the same arguments as above.
Discrete charges
If the charge in a region consists of N discrete point-like charge carriers like electrons the charge density can be expressed via the Dirac delta function, for example, the volume charge density is:
 ;
;
where 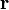 is the test position,
is the test position, is the charge of the ith charge carrier, whose position is
is the charge of the ith charge carrier, whose position is  .
.
If all charge carriers have the same charge q (for electrons q = − e) the charge density can be expressed through the charge carrier density  : Again, the equivalent equations for the linear and surface charge densities follow directly from the above relations.
: Again, the equivalent equations for the linear and surface charge densities follow directly from the above relations.
[]Quantum charge densitY
In quantum mechanics, charge density is related to wavefunction  by the equation
by the equation
when the wavefunction is normalized as